Spiral cone

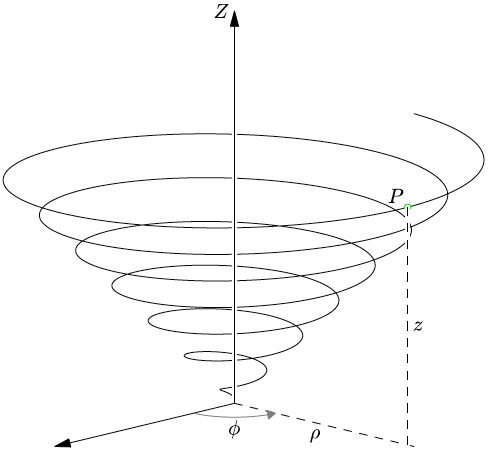
\documentclass[border=10pt]{standalone}
\usepackage[inline]{asymptote}
\begin{document}
\begin{asy}
settings.render = 0;
settings.prc = false;
import graph3;
real unit = 0.1cm;
unitsize(unit);
defaultpen(fontsize(10pt));

triple eyeDirection = dir((-2,-2,0.7));
currentprojection = orthographic(eyeDirection);
triple translateDirection = dir(cross(Z, eyeDirection));

void drawBehind(path3 thepath, pen pen=currentpen, real backOpacity = 1.0, real backWidth=2.0)
{
  real newsize = backWidth;
  real distBehind = (newsize/2 + linewidth(pen)/2 + 10) * (1bp/unit);
  draw(shift(-distBehind*dir(eyeDirection))*thepath, white+linewidth(newsize)+opacity(backOpacity));
}

real r(real t) { return t; }
real z(real t) { return t; }
real theta(real t) { return t; }

triple F(real t) {
  real r = r(t);
  real z = z(t);
  real theta = theta(t);
  return (r*cos(theta), r*sin(theta), z);
}

path3 p = graph(F, 0, 7*2pi, operator ..);

drawBehind(p);
draw(p);
drawBehind((0,0,0) -- (0,0,70));
draw((0,0,0) -- (0,0,70), arrow=Arrow3());
label("$Z$", position=(0,0,70), align=W);

triple point = F((6 + 3/4)*2pi);
dot(point, green);
label("$P$", position=point, align=NW);

draw(O -- -7*2pi*X, arrow=Arrow3());
draw(O -- -7*2pi*Y, dashed);
label(position=-7pi*Y, "$\rho$", align=SW);

path3 arc = arc(O, -10X, -10Y);
draw(arc, arrow=ArcArrow3(), gray);
label(position=relpoint(arc,0.5), "$\phi$", align=0.5S);

drawBehind((point.x,point.y,0) -- point);
draw((point.x,point.y,0) -- point, dashed);
label(position=scale(1,1,0.5)*point, "$z$", align=E);

shipout(scale(4)*currentpicture.fit());
\end{asy}
\end{document}

Source: TeX.SE
Author: Charles Staats (License)