Cubes

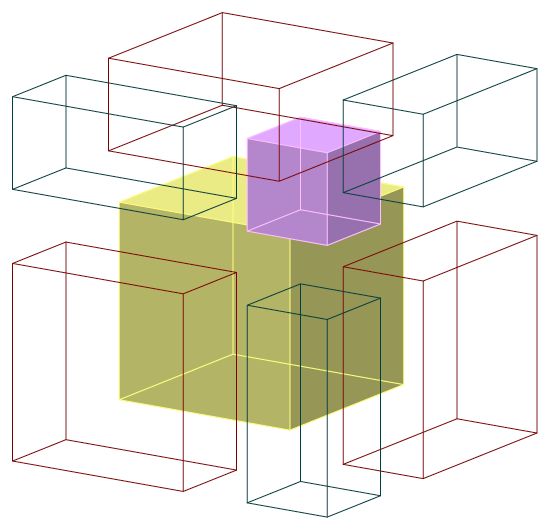
This solution illustrates (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3.

\documentclass[border=10pt]{standalone}
\usepackage[inline]{asymptote}
\begin{document}
\begin{asy}[width=\the\linewidth,inline=true]
settings.outformat="pdf";
settings.render=0;
settings.prc=false;
unitsize(1cm);
import three;
currentprojection=orthographic(3,2,1,center=true,zoom=.8);
//currentprojection=orthographic(0,10,0,zoom=.8);
light White=light(new pen[] {rgb(0.38,0.38,0.45),rgb(0.6,0.6,0.67),
                             rgb(0.5,0.5,0.57)},specularfactor=3,
  new triple[] {(5,5,5),(0,5,5),(-0.5,0,2)});

currentlight=White;

real a=3.2, b=1.5;
path3[] p=unitbox;
surface q=unitcube;
void mybox(triple A, triple B, pen fillpen=nullpen,
pen drawpen=nullpen,triple shifting=O){
real s=(abs(B-A))/sqrt(3);  
draw(shift(shifting)*shift(A)*scale3(s)*q,fillpen+opacity(1));
draw(shift(shifting)*box(A,B),drawpen);
}
triple A=(-a,-a,-a);  // lower vertex
triple B=(b,b,b);     // upper vertex
pen pena=lightyellow; // for a^3
pen penb=pink;        // for b^3
pen pena2b=brown;     // for 3 a^2 b
pen penab2=darkcyan;  // for 3 a b^2
real t=.6;            // for shifting boxes

mybox(A,O,pena,pena);
mybox(O,B,penb,penb,(t,t,t));

// 3 a^2 b
draw(shift(t,-t,-t)*box(O,(b,-a,-a)),pena2b);
draw(shift(-t,-t,t)*box(O,(-a,-a,b)),pena2b);
draw(shift(-t,t,-t)*box(O,(-a,b,-a)),pena2b);

// 3 a b^2
draw(shift(t,t,-t)*box(O,(b,b,-a)),penab2);
draw(shift(-t,t,t)*box(O,(-a,b,b)),penab2);
draw(shift(t,-t,t)*box(O,(b,-a,b)),penab2);
\end{asy}
\end{document}

Source: TeX.SE

Author: Black Mild (License)