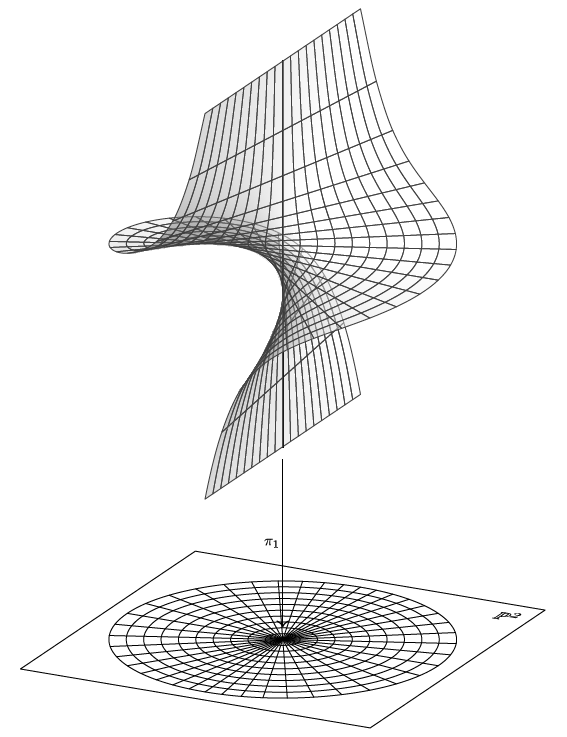
The following image illustrates the blowup of a plane at a point–an important construction in algebraic geometry.
\documentclass[border=10pt]{standalone}
\usepackage[inline]{asymptote}
\begin{document}
\begin{asy}[width=\the\linewidth,inline=true]
settings.outformat="pdf";
settings.render=0;
settings.prc=false;
usepackage("lmodern");
usepackage("fontenc","T1");
usepackage("amssymb"); // for the \mathbb command
defaultpen(fontsize(10pt));
import graph3;
size(400,400);
currentprojection=orthographic(5,-10,4);
real R=8;
struct scaler {
private real factor;
void operator init(real factor) {
this.factor = factor;
}
real scale(real t) {return factor*atan(tan(t)/factor);}
real invert(real t) {return tan(atan(t)*factor)/factor;}
}
scaler theScaler = scaler(6);
triple f(pair t) {
real r = t.x;
real theta = 2 * atan(t.y*2/pi);
// real theta = -t.y;
return (r*cos(theta),r*sin(theta),theScaler.scale(theta));
}
int resolution = 10;
real epsilon = .01;
real vmin = -pi/2;
real vmax = pi/2;
real umin = -R;
real umax = R;
splinetype[] Linear = new splinetype[] {linear, linear, linear};
splinetype[] ZMonotonic = new splinetype[] {notaknot, notaknot, monotonic};
surface sBack=surface(f,(umin,vmin),(0,vmax),nu=resolution, nv=2*resolution, usplinetype=Linear, vsplinetype = ZMonotonic);
surface sFront = surface(f, (0,vmin), (umax,vmax), nu=resolution, nv=2*resolution, usplinetype=Linear, vsplinetype=ZMonotonic);
pen meshpen = heavygray + linewidth(0.2);
material surfacepen =
material(diffusepen=lightgray+opacity(0.5),
emissivepen=gray(0.3),
specularpen=gray(0.2));
draw(sBack, surfacepen=surfacepen, meshpen=meshpen);
draw(f((0,vmin)) -- f((0,vmax)), darkgray+linewidth(1.0)); // the exceptional divisor
draw(sFront, surfacepen=surfacepen, meshpen=meshpen);
pen planePen = black+linewidth(0.3);
triple bottomPoint = f((0,vmin));
triple planeCenter = 2.0*bottomPoint;
draw((bottomPoint-.6Z)--(planeCenter+.6Z), arrow=Arrow3(TeXHead2), p=linewidth(0.9),
L="$\pi_1$");
real planeZ = planeCenter.z;
triple h(pair t) {
return (t.x, t.y, planeZ);
}
triple g(pair t) {
triple projectFrom = f(t);
return h((projectFrom.x, projectFrom.y));
}
triple g(real tx, real ty) { return g((tx, ty)); }
real planeRadius = R+1;
surface thePlane = surface(h, (-planeRadius,-planeRadius),(planeRadius,planeRadius),
nu=1);
path3 planeOutline = h((-planeRadius,-planeRadius)) -- h((-planeRadius,planeRadius)) -- h((planeRadius,planeRadius)) -- h((planeRadius,-planeRadius)) -- cycle;
for (real u = 0; u <= R; u += R/resolution)
draw(circle(planeCenter, u), planePen);
for (real v = vmin; v < vmax; v += (vmax-vmin)/(2*resolution)) {
draw(g(umin,v) -- g(umax,v), planePen);
}
draw(planeOutline, p=planePen);
//Embed the label "\mathbb P^2" on the plane:
real labelScale = 1.5;
Label planeLabel = Label(scale(labelScale, labelScale*1.3, 1)*"$\mathbb P^2$", fontsize(10pt));
Label placedPlaneLabel = shift((planeRadius-1.2),(planeRadius-1.5),planeCenter.z)*planeLabel;
label(planeLabel, position = (planeRadius-1.2, planeRadius-1.5, planeCenter.z));
\end{asy}
\end{document}
Source: TeX.SE
Author: Charles Staats (License)